Calcula fácilmente las medidas de tendencia central: guía completa sobre cómo obtener resultados precisos

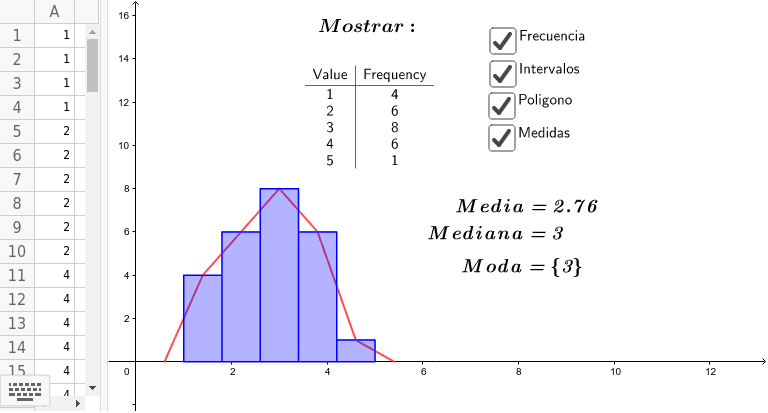
Las medidas de tendencia central son estadísticas que nos ayudan a entender y resumir un conjunto de datos. Son herramientas clave en el análisis de datos y nos brindan información sobre el valor central o típico de un conjunto de datos. Entre las medidas de tendencia central más comunes se encuentran la media, la mediana y la moda.

Aprenderemos cómo calcular estas medidas y qué información proporciona cada una de ellas. Descubriremos cómo obtener resultados precisos y cuándo utilizar cada medida según las características de nuestros datos. También exploraremos algunos ejemplos prácticos para ver cómo se aplican estas medidas en situaciones reales. Ya sea que estés estudiando estadística, trabajando con datos en tu trabajo o simplemente interesado en aprender más sobre este tema, esta guía completa te ayudará a dominar las medidas de tendencia central. ¡Comencemos!

Qué son las medidas de tendencia central

Las medidas de tendencia central son estadísticas que se utilizan para describir el centro o la posición central de un conjunto de datos. También se conocen como medidas de localización, ya que indican dónde se encuentra ubicado el valor central o típico del conjunto de datos.

Existen varias medidas de tendencia central comúnmente utilizadas, entre las que se incluyen:

• La media aritmética
• La mediana
• La moda
• La media ponderada
• El percentil

La media aritmética

La media aritmética, o simplemente la media, es la medida de tendencia central más común. Se calcula sumando todos los valores del conjunto de datos y dividiendo ese resultado entre el número total de valores.


media = suma de los valores / número de valores


Por ejemplo, si tenemos los siguientes datos: 2, 4, 6, 8, 10, la media sería:


media = (2 + 4 + 6 + 8 + 10) / 5 = 6


La mediana

La mediana es el valor central en un conjunto ordenado de datos. Para calcularla, primero se deben ordenar los datos de menor a mayor, y luego encontrar el valor que se encuentra en medio. Si hay un número impar de datos, la mediana será el valor que divide al conjunto en dos mitades iguales. Si hay un número par de datos, la mediana será el promedio de los dos valores centrales.

Por ejemplo, si tenemos los siguientes datos: 2, 4, 6, 8, 10, la mediana sería:


mediana = 6


La moda

La moda es el valor que aparece con mayor frecuencia en un conjunto de datos. Puede haber una moda (unimodal), dos modas (bimodal) o más modas (multimodal). También puede darse el caso en el que no haya ninguna moda, es decir, que todos los datos sean distintos.

Por ejemplo, si tenemos los siguientes datos: 2, 3, 3, 4, 5, 5, 5, 6, la moda sería:


moda = 5


La media ponderada

La media ponderada es similar a la media aritmética, pero se le asigna un peso o importancia diferente a cada valor del conjunto de datos. Para calcularla, se multiplica cada valor por su respectivo peso, se suman todos estos productos y se divide el resultado entre la suma de los pesos.


media_ponderada = (valor1 * peso1 + valor2 * peso2 + ... + valorn * peson) / (peso1 + peso2 + ... + peson)


El percentil

El percentil indica el valor por debajo del cual se encuentra un determinado porcentaje de los datos. Por ejemplo, el percentil 75 indica el valor por debajo del cual se encuentra el 75% de los datos. Se calcula ordenando los datos de menor a mayor, y luego encontrando el valor que corresponde al percentil deseado.

Por ejemplo, si tenemos los siguientes datos: 2, 4, 6, 8, 10, y queremos calcular el percentil 75, primero ordenamos los datos:


2, 4, 6, 8, 10


Luego, calculamos cuántos datos se encuentran por debajo del percentil 75:


(75 / 100) * 5 = 3.75


Como 3.75 está entre los valores 4 y 6, podemos interpolar para encontrar el percentil exacto:


percentil 75 ≈ 4 + (6 - 4) * 0.75 = 5.5


Estas son las principales medidas de tendencia central que se utilizan para describir un conjunto de datos. Son herramientas fundamentales en el análisis estadístico y permiten obtener una representación concisa y significativa de la distribución de los datos.

Cuáles son las medidas de tendencia central más comunes

En estadística, las medidas de tendencia central se utilizan para resumir y describir un conjunto de datos. Son valores que representan el centro o la ubicación típica de los datos. Las medidas de tendencia central más comunes son:

• Media: también conocida como promedio, es la suma de todos los valores dividida por el número total de elementos en el conjunto de datos. Se calcula sumando todos los valores y luego dividiendo entre el tamaño del conjunto de datos.
• Mediana: es el valor medio en un conjunto de datos ordenados. Se encuentra ubicando el valor en el centro de la distribución. Si el conjunto de datos tiene un número impar de elementos, la mediana será el valor en el medio. Si el conjunto de datos tiene un número par de elementos, la mediana será el promedio de los dos valores centrales.
• Moda: es el valor que aparece con mayor frecuencia en un conjunto de datos. Puede haber una moda única o múltiples modas en un conjunto de datos. Un conjunto de datos puede no tener una moda si no hay valores repetidos.

Estas medidas proporcionan información sobre la distribución y comportamiento de los datos. Son esenciales para comprender y analizar conjuntos de datos y se utilizan ampliamente en diferentes campos como la economía, la psicología, la biología y muchas otras disciplinas.

Cómo se calcula la media aritmética

El cálculo de la media aritmética es uno de los métodos más comunes para obtener una medida de tendencia central en un conjunto de datos. Para calcular la media aritmética, debemos sumar todos los valores del conjunto y luego dividir el resultado entre el número total de elementos.

Veamos un ejemplo: supongamos que tenemos el siguiente conjunto de datos:

1, 2, 3, 4, 5

Para calcular la media aritmética, sumamos todos los valores:

1 + 2 + 3 + 4 + 5 = 15

Luego, dividimos la suma por el número de elementos (en este caso, 5):

15 / 5 = 3

Por lo tanto, la media aritmética de este conjunto de datos es 3.

Fórmula de la media aritmética

La fórmula general para calcular la media aritmética es la siguiente:

media = (x1 + x2 + ... + xn) / n

Donde x1, x2, ..., xn son los valores del conjunto y n es el número total de elementos.

Cabe mencionar que la media aritmética se ve afectada por los valores atípicos o outliers, ya que al sumar todos los valores, estos influyen en el resultado final.

Cuándo es útil utilizar la mediana en lugar de la media

La mediana es una medida de tendencia central que se utiliza para representar el valor central de un conjunto de datos ordenados. A diferencia de la media, que se calcula sumando todos los valores y dividiendo entre el número total de elementos, la mediana se obtiene encontrando el valor que divide al conjunto en dos partes iguales.

Hay situaciones en las que utilizar la mediana en lugar de la media es más útil y adecuado. Uno de los casos más comunes es cuando tenemos un conjunto de datos con valores extremos o atípicos. Estos valores pueden afectar significativamente el cálculo de la media, ya que se ven muy influenciados por ellos. Al utilizar la mediana, estos valores extremos no tienen tanto peso, ya que solo afectan a un único valor dentro del conjunto ordenado.

Otra situación en la que la mediana es preferible a la media es cuando el conjunto de datos es asimétrico o presenta una distribución no normal. La media puede verse afectada por valores atípicos y causar una distorsión en la representación del centro del conjunto de datos. En cambio, la mediana es una medida más robusta, que se ve menos afectada por este tipo de distribuciones y proporciona una mejor estimación del valor central.

Utilizar la mediana en lugar de la media es útil cuando se requiere una medida más resistente a valores extremos o atípicos, o cuando se trabaja con distribuciones no normales. Es importante tener en cuenta el contexto y objetivo del análisis estadístico para elegir la medida de tendencia central más apropiada.

Cómo se calcula la moda y cuándo se utiliza

La moda es una medida de tendencia central que representa el valor o valores con mayor frecuencia en un conjunto de datos. Se utiliza principalmente cuando se quiere identificar el valor más común o representativo de un conjunto de datos.

Para calcular la moda, se deben seguir los siguientes pasos:

1. Ordenar los datos: Primero, es importante ordenar los datos en orden ascendente o descendente. Esto facilitará la identificación del valor (o valores) con mayor frecuencia.
2. Contar las repeticiones: A continuación, se deben contar las repeticiones de cada valor en el conjunto de datos ordenado. Esto implica identificar cuántas veces aparece cada valor en la lista.
3. Identificar el valor con mayor frecuencia: Una vez se han contado todas las repeticiones, se debe identificar cuál valor o valores tienen la mayor frecuencia. Estos serán la(s) moda(s) del conjunto de datos.

Es importante tener en cuenta que un conjunto de datos puede tener una moda única, donde solo hay un valor con la mayor frecuencia, o múltiples modas, donde varios valores tienen la misma frecuencia máxima.

Un ejemplo práctico de cómo calcular la moda es el siguiente:

Supongamos que se tiene el siguiente conjunto de datos: 5, 8, 3, 2, 8, 6, 8.

Primero, se ordenan los datos de forma ascendente: 2, 3, 5, 6, 8, 8, 8.

A continuación, se cuentan las repeticiones de cada valor:

• El número 2 aparece una vez.
• El número 3 aparece una vez.
• El número 5 aparece una vez.
• El número 6 aparece una vez.
• El número 8 aparece tres veces.

Finalmente, se identifica que el valor con mayor frecuencia es el 8, ya que este aparece tres veces en el conjunto de datos. Por lo tanto, la moda de este conjunto de datos es 8.

La moda es un cálculo relativamente sencillo que permite identificar el valor o valores con mayor frecuencia en un conjunto de datos. Su cálculo implica ordenar los datos, contar las repeticiones y determinar cuál valor o valores tienen la frecuencia más alta.

Qué es la media ponderada y cómo se calcula

La media ponderada es una medida de tendencia central que se utiliza para calcular un promedio considerando el peso o importancia de cada valor en función de su frecuencia o relevancia en relación a los demás.

Para calcular la media ponderada, primero se deben asignar pesos a cada valor en función de su importancia relativa. Luego, se multiplica cada valor por su respectivo peso y se suman todos los productos resultantes. Finalmente, se divide esta suma por la suma de los pesos.

A continuación, se muestra una fórmula general para calcular la media ponderada:

Media ponderada = (valor1 * peso1 + valor2 * peso2 + ... + valorn * peson) / (peso1 + peso2 + ... + peson)

Es importante destacar que los pesos deben ser valores no negativos y la suma de los pesos debe ser diferente de cero. Además, es fundamental definir correctamente los criterios de ponderación para obtener resultados precisos y relevantes en función del contexto en el que se esté aplicando esta medida de tendencia central.

La media ponderada es especialmente útil cuando se desea dar mayor importancia a algunos valores sobre otros, o cuando se quiere tener en cuenta el impacto que tienen ciertos datos en el resultado final.

Por ejemplo, si se quiere calcular la calificación promedio de un estudiante considerando que las tareas tienen un peso del 30%, los exámenes parciales un 40% y el examen final un 30%, se podrían asignar los siguientes pesos: 0.3, 0.4 y 0.3 respectivamente. Luego, se multiplicaría cada valor de calificación por su peso correspondiente, se sumarían todos los productos y finalmente se dividiría entre la suma de los pesos.

Cuál es la diferencia entre la media, la mediana y la moda

En estadística, la media, la mediana y la moda son medidas de tendencia central que se utilizan para describir y resumir conjuntos de datos. Cada una de estas medidas tiene diferentes propiedades y se calcula de manera distinta, pero todas ellas nos ofrecen información valiosa sobre los valores centrales de un conjunto de datos.

Media:

La media es el valor promedio de un conjunto de datos. Se calcula sumando todos los valores del conjunto y dividiendo el resultado entre la cantidad de elementos. La fórmula para calcular la media es la siguiente:

media = (suma de todos los valores) / (cantidad de elementos)

La media es una medida sensible a los valores extremos, ya que incorpora todos los valores en su cálculo. Por lo tanto, si hay valores atípicos en el conjunto de datos, la media puede ser afectada significativamente. Sin embargo, en muchas situaciones, la media es una medida útil y representa bien el conjunto de datos en su conjunto.

Mediana:

La mediana es el valor medio de un conjunto de datos cuando estos se encuentran ordenados de menor a mayor. Para calcular la mediana, primero se ordenan los valores y luego se encuentra el valor central. Si el conjunto de datos tiene un número impar de elementos, el valor central será simplemente el valor que se encuentre en medio. Si el conjunto de datos tiene un número par de elementos, la mediana será igual al promedio de los dos valores centrales.

Para calcular la mediana, primero se ordena el conjunto de datos y luego se aplica la siguiente regla:

• Si el número de elementos es impar, la mediana es el valor que se encuentra exactamente en el medio del conjunto ordenado.
• Si el número de elementos es par, la mediana es el promedio de los dos valores que se encuentran en el medio del conjunto ordenado.

La mediana es una medida robusta a los valores extremos, ya que solo depende de los valores centrales y no tiene en cuenta los valores extremos. Es especialmente útil cuando se presentan datos sesgados o con valores atípicos.

Moda:

La moda es el valor o los valores que más se repiten en un conjunto de datos. Si un conjunto de datos tiene una moda, se dice que es unimodal; si tiene dos modas, se dice que es bimodal; y si tiene más de dos modas, se dice que es multimodal. Sin embargo, también puede ocurrir que un conjunto de datos no tenga moda, es decir, que todos los valores sean distintos y no haya repetición alguna.

Para calcular la moda, se pueden utilizar métodos gráficos como el histograma o el diagrama de barras, o simplemente observar cuál es el valor o los valores que tienen mayor frecuencia en el conjunto de datos. En algunos casos, un conjunto de datos puede tener varias modas o ninguna. La moda es una medida útil para identificar los valores más frecuentes o representativos dentro del conjunto de datos.

Cuál es la importancia de las medidas de tendencia central en el análisis de datos

Las medidas de tendencia central son herramientas fundamentales en el análisis de datos, ya que nos permiten resumir y comprender la distribución de valores en un conjunto de datos. Estas medidas proporcionan información sobre el valor central o típico de un conjunto de datos, lo que nos ayuda a tener una idea general de cómo se distribuyen los datos alrededor de ese valor central.

La importancia de estas medidas radica en que nos permiten resumir un conjunto de datos en un solo número o valor, lo que facilita su interpretación y comparación. Además, estas medidas nos ayudan a identificar valores atípicos o extremos en los datos, lo que puede ser crucial para detectar errores en la medición o anomalías en los datos recopilados.

Existen varias medidas de tendencia central comúnmente utilizadas, como la media aritmética, la mediana y la moda. Cada una de estas medidas tiene sus propias características y aplicaciones, por lo que es importante comprender cómo calcular y utilizar cada una de ellas de manera adecuada.

Las medidas de tendencia central son esenciales en el análisis de datos porque nos permiten resumir y comprender la distribución de valores en un conjunto de datos. Estas medidas facilitan la interpretación y comparación de datos, y nos ayudan a identificar valores atípicos o extremos. En esta guía completa, te mostraremos cómo calcular y utilizar correctamente las medidas de tendencia central para obtener resultados precisos en tus análisis de datos.

Cuáles son las limitaciones de las medidas de tendencia central

Las medidas de tendencia central son herramientas estadísticas utilizadas para resumir y describir conjuntos de datos en un solo valor representativo. Sin embargo, es importante tener en cuenta que estas medidas tienen sus limitaciones y no siempre proporcionan una imagen completa de la distribución de los datos. A continuación se presentan algunas de las limitaciones más comunes de las medidas de tendencia central:

1. Sensibilidad a valores extremos

Las medidas de tendencia central pueden verse afectadas significativamente por valores extremos o atípicos en los datos. Por ejemplo, la media aritmética puede ser sesgada por la presencia de valores extremadamente altos o bajos. Esto puede llevar a conclusiones erróneas si no se tienen en cuenta estos valores atípicos al interpretar los resultados.

2. Ignora la forma de la distribución

Las medidas de tendencia central no tienen en cuenta la forma de la distribución de los datos. Pueden ignorar diferencias importantes en la dispersión y asimetría de los datos. Por ejemplo, dos conjuntos de datos pueden tener la misma media pero diferentes variabilidades o características de distribución.

3. No representa adecuadamente datos no numéricos

Algunas medidas de tendencia central, como la media aritmética, sólo son aplicables a datos numéricos. Si se aplican a datos no numéricos, los resultados pueden carecer de sentido o ser difíciles de interpretar. Además, estas medidas tampoco consideran información contextual o cualitativa que podría ser relevante en el análisis de los datos no numéricos.

4. Limitado a datos unidimensionales

Las medidas de tendencia central son más adecuadas para analizar datos unidimensionales, es decir, datos que tienen una sola variable independiente. Si se tienen datos multidimensionales o datos con múltiples variables independientes, las medidas de tendencia central pueden no ser suficientes para proporcionar una descripción completa de los datos.

5. No considera la presencia de valores ausentes

Las medidas de tendencia central pueden verse afectadas por la presencia de valores ausentes en los datos. Si no se tiene en cuenta correctamente la presencia de valores ausentes, los resultados pueden ser sesgados y conducir a conclusiones incorrectas. Es importante manejar los valores ausentes de manera adecuada antes de calcular y analizar las medidas de tendencia central.

Qué otros métodos existen para analizar la dispersión de los datos

Además de calcular las medidas de tendencia central, existen otros métodos que nos permiten analizar la dispersión de los datos. Estos métodos nos darán una idea de qué tan dispersos están los datos alrededor de la medida central.

Rango

El rango es una medida de dispersión que se obtiene restando el valor máximo del conjunto de datos al valor mínimo. Es la forma más sencilla de medir la dispersión, ya que no toma en cuenta todos los valores individuales, sino solo los extremos.

rango = valor_maximo - valor_minimo

Desviación estándar

La desviación estándar es una medida de dispersión que indica cuánto varían los datos con respecto a la media. Se calcula obteniendo la raíz cuadrada de la varianza.

desviacion_estandar = sqrt(varianza)

Varianza

La varianza es otra medida de dispersión que representa qué tanto se alejan los datos individuales de la media. Se calcula sumando los cuadrados de las diferencias entre cada dato y la media, y dividiendo este resultado por la cantidad total de datos.

varianza = (sumatoria((dato - media)^2)) / cantidad de datos

Coeficiente de variación

El coeficiente de variación es una medida de dispersión relativa, que permite comparar la dispersión de diferentes conjuntos de datos. Se calcula dividiendo la desviación estándar por la media y multiplicando el resultado por 100.

coeficiente_de_variacion = (desviacion_estandar / media) * 100

Diagramas de caja y bigotes

Los diagramas de caja y bigotes, también conocidos como boxplots, son herramientas visuales que nos permiten identificar la dispersión de los datos de manera gráfica. Estos diagramas representan cuartiles, mediana, valores mínimos y máximos, e incluso pueden mostrar posibles valores atípicos o outliers.

Al calcular las medidas de tendencia central es importante tener en cuenta también las medidas de dispersión, ya que nos proporcionan información valiosa sobre cómo se distribuyen los datos a lo largo del conjunto. Existen diferentes métodos para analizar la dispersión, desde el rango hasta el coeficiente de variación, y también podemos utilizar herramientas visuales como los diagramas de caja y bigotes.

Cómo interpretar los resultados obtenidos al calcular medidas de tendencia central

Al calcular medidas de tendencia central, es importante poder interpretar los resultados obtenidos para poder comprender la distribución de los datos y tomar decisiones informadas. Aquí te presentamos una guía completa sobre cómo interpretar correctamente los resultados obtenidos al calcular las medidas de tendencia central.

Media aritmética

La media aritmética es la medida de tendencia central más comúnmente utilizada. Representa el promedio de los valores observados en un conjunto de datos. Para interpretar correctamente la media aritmética, debemos tener en cuenta lo siguiente:

1. Si la media es igual a cero, significa que los valores observados se equilibran en torno a cero.
2. Si la media es mayor que cero, indica que los valores observados tienden a estar por encima de cero.
3. Si la media es menor que cero, sugiere que los valores observados están por debajo de cero.
4. Si la media es igual al valor máximo del conjunto de datos, implica que hay uno o varios valores atípicos.
5. Si la media es igual a la mediana, significa que los datos están simétricamente distribuidos.

Mediana

La mediana es el valor medio en un conjunto de datos ordenados de forma ascendente o descendente. La interpretación de la mediana se basa en los siguientes puntos:

• Si la mediana es igual a la media, implica una distribución simétrica de los datos.
• Si la mediana está más cerca del valor mínimo que del valor máximo, sugiere una asimetría negativa de los datos (cola a la izquierda).
• Si la mediana está más cerca del valor máximo que del valor mínimo, indica una asimetría positiva de los datos (cola a la derecha).

Moda

La moda es el valor que ocurre con mayor frecuencia en un conjunto de datos. Al interpretar la moda, se deben considerar las siguientes situaciones:

• Si hay una única moda, indica que el valor más común del conjunto de datos es único.
• Si hay múltiples modas, significa que el conjunto de datos tiene varios valores que ocurren con la misma frecuencia máxima.
• Si no hay moda, se dice que los datos tienen una distribución uniforme sin valores que se destaquen por su frecuencia.

Al interpretar correctamente los resultados obtenidos al calcular las medidas de tendencia central, podremos entender mejor la distribución de los datos y hacer inferencias más precisas.

Cuándo es apropiado utilizar medidas de tendencia central en diferentes escenarios

Las medidas de tendencia central son utilizadas con frecuencia en diversos escenarios donde se requiere analizar un conjunto de datos para entender su comportamiento y obtener conclusiones sobre la distribución de los mismos. A continuación, se presentan algunos ejemplos de cuándo es apropiado utilizar estas medidas:

Análisis estadístico de una muestra

Cuando se trabaja con una muestra representativa de una población, las medidas de tendencia central son muy útiles para resumir los datos y obtener una idea general de cómo se distribuyen. Por ejemplo, si se realiza un estudio sobre la altura de los estudiantes de una escuela, encontrar la media o la mediana permitirá conocer la altura promedio o la altura que se encuentra en el centro de la muestra respectivamente.

Comparación de grupos o categorías

En situaciones donde es necesario comparar diferentes grupos o categorías, las medidas de tendencia central pueden proporcionar información clave. Por ejemplo, al analizar los salarios de empleados de diferentes departamentos de una empresa, encontrar la media o la moda puede ayudar a identificar si hay diferencias significativas entre los grupos.

Predicción y proyecciones

Al realizar predicciones o proyecciones, conocer las medidas de tendencia central puede ser de gran utilidad para estimar valores futuros. Por ejemplo, al analizar el crecimiento de ventas de un producto durante varios años, encontrar la tasa de cambio promedio o la mediana de las ventas puede servir como punto de partida para proyectar futuras ganancias.

Detección de valores atípicos

Las medidas de tendencia central también se utilizan para identificar valores atípicos o extremos en un conjunto de datos. Por ejemplo, al analizar los precios de viviendas en un vecindario, detectar la media y la desviación estándar permitirá identificar si existen propiedades con precios significativamente más altos o más bajos que el promedio.

Las medidas de tendencia central son apropiadas en diversos escenarios donde se necesita resumir y comprender un conjunto de datos. Su uso permite obtener resultados precisos que pueden ayudar en la toma de decisiones, comparaciones y proyecciones.

Qué precauciones se deben tener en cuenta al calcular medidas de tendencia central

Al calcular medidas de tendencia central, es importante tener en cuenta algunas precauciones para obtener resultados precisos y confiables. Estas precauciones son especialmente relevantes cuando se trabaja con conjuntos de datos que presentan características particulares o cuando se busca una interpretación específica de los resultados.

1. Considerar la distribución de los datos

Es fundamental analizar la distribución de los datos antes de calcular cualquier medida de tendencia central. Si los datos siguen una distribución normal, las medidas más comunes como la media aritmética o la mediana pueden ser adecuadas. Sin embargo, si la distribución es sesgada o presenta valores atípicos, es posible que sea necesario utilizar medidas más robustas, como la media truncada o la mediana ponderada.

2. Eliminar valores atípicos

Los valores atípicos pueden afectar significativamente las medidas de tendencia central, especialmente la media aritmética. Antes de realizar cualquier cálculo, es recomendable identificar y eliminar estos valores. Esto se puede hacer utilizando diferentes métodos, como el rango intercuartílico o los diagramas de caja y bigote.

3. Verificar la validez de los datos

Es importante asegurarse de que los datos utilizados sean válidos y representativos de la población o muestra en estudio. En ocasiones, pueden existir errores de entrada, mediciones incorrectas o datos incompletos que afecten la precisión de los resultados. Realizar una revisión exhaustiva de los datos antes de realizar cualquier cálculo es fundamental.

4. Utilizar medidas complementarias

En muchas ocasiones, una única medida de tendencia central no es suficiente para describir completamente los datos. Es recomendable utilizar medidas complementarias, como la desviación estándar o el rango intercuartílico, que aporten información adicional sobre la dispersión o la variabilidad de los datos.

5. Considerar el tamaño de la muestra

El tamaño de la muestra puede influir en las medidas de tendencia central. Mientras más grande sea la muestra, mayor será la precisión y representatividad de las medidas estimadas. Sin embargo, es importante tener en cuenta que existen casos en los que incluso con una muestra pequeña se pueden obtener resultados confiables, siempre y cuando se cumplan los supuestos necesarios.

6. Interpretar adecuadamente los resultados

No basta con calcular las medidas de tendencia central, es fundamental interpretar adecuadamente los resultados. Las medidas de tendencia central son solo una parte del análisis estadístico y deben ser complementadas con otros análisis y consideraciones. Es importante contextualizar los resultados dentro del problema de investigación o estudio y evitar extrapolar conclusiones sin fundamentos sólidos.

Preguntas frecuentes (FAQ)

1. ¿Qué son las medidas de tendencia central?

Las medidas de tendencia central son estadísticas que se utilizan para resumir y describir un conjunto de datos en términos de su valor central o típico.

2. ¿Cuáles son las medidas de tendencia central más comunes?

Las medidas de tendencia central más comunes son la media, la mediana y la moda.

3. ¿Cuándo debo usar la media como medida de tendencia central?

La media se utiliza cuando los datos tienen una distribución simétrica y no hay valores atípicos que puedan afectar significativamente el resultado.

4. ¿Cuándo debo usar la mediana como medida de tendencia central?

La mediana se utiliza cuando los datos tienen una distribución sesgada o existen valores atípicos que podrían distorsionar el resultado si se utiliza la media.

5. ¿Cuándo debo usar la moda como medida de tendencia central?

La moda se utiliza cuando los datos son categóricos o discretos, y se busca identificar el valor más frecuente o repetido en el conjunto de datos.