Descubre cómo sacar la inversa de una función y mejora tus habilidades matemáticas ahora mismo

En el mundo de las matemáticas, muchas veces se nos presenta la necesidad de encontrar la inversa de una función. La inversa de una función es otra función que deshace la acción de la función original. Es decir, si aplicamos la función y luego aplicamos su inversa, deberíamos obtener el valor de partida. En otras palabras, la función y su inversa se "anulan" entre sí.

Exploraremos en detalle cómo sacar la inversa de una función y qué estrategias podemos utilizar para simplificar este proceso. Veremos los diferentes casos posibles, resolveremos ejemplos paso a paso y discutiremos algunas propiedades y conceptos importantes relacionados con las funciones y sus inversas. Así que prepárate para fortalecer tus habilidades matemáticas y descubrir un nuevo mundo de relaciones entre las funciones.

Qué es la inversa de una función y por qué es importante conocerla

La inversa de una función es una operación matemática que nos permite obtener el valor original de una variable a partir del resultado de la función. Es decir, si tenemos una función f(x) que transforma un número x en otro número y, la inversa de esa función, denotada como f^-1(y), nos permite encontrar el valor de x que generó ese resultado y.

Conocer la inversa de una función es fundamental en el estudio de las matemáticas, ya que nos permite resolver problemas de forma más eficiente y comprender mejor las relaciones entre las variables. Por ejemplo, si estamos evaluando una función en cierto valor y queremos saber qué valor de entrada lo generó, podemos utilizar la inversa para hallar esa respuesta de manera directa.

Además, la inversa de una función también es útil para determinar si una función es biyectiva o no. Una función es biyectiva cuando cada elemento del conjunto de salida tiene un único preimagen en el conjunto de entrada. Esto implica que si una función tiene una inversa, entonces es biyectiva.

La inversa de una función nos ayuda a entender mejor las relaciones entre variables, nos permite resolver problemas de forma más eficiente y determinar si una función es biyectiva. A continuación, veremos cómo se calcula la inversa de una función.

Cómo determinar si una función tiene una inversa

Antes de aprender a sacar la inversa de una función, es importante determinar si la función en cuestión tiene una inversa. No todas las funciones cuentan con una inversa, por lo que es fundamental verificar esta condición antes de intentar calcularla.

Para determinar si una función tiene una inversa, se aplica una prueba básica conocida como la prueba de la horizontalidad de la función. Esta prueba se basa en el concepto de que una función y su inversa deben pasar la prueba de intercambiabilidad, es decir, que al reemplazar en la función original los valores de x por los valores de y obtengamos nuevamente los valores de y.

La prueba consiste en graficar la función en un plano cartesiano y ver si la gráfica pasa la llamada “prueba de línea horizontal”. Esta prueba se realiza trazando una línea horizontal en el gráfico de la función y luego observando si dicha línea intersecta la gráfica en más de un punto. Si la línea horizontal intersecta la gráfica solo en un punto, entonces la función tiene una inversa. Por el contrario, si la línea horizontal intersecta la gráfica en dos o más puntos, la función no tiene una inversa, ya que no cumple con el requisito de la prueba.


function tieneInversa(function) {
// Graficar la función
plot(function);

// Dibujar línea horizontal
drawHorizontalLine();

// Contar puntos de intersección
var intersecciones = contarIntersecciones();

// Verificar resultado
if (intersecciones === 1) {
return true;
} else {
return false;
}
}


En el código de arriba, podemos ver una posible implementación de cómo determinar si una función tiene una inversa. Primero, se grafica la función en un plano cartesiano utilizando algún software o librería que permita hacerlo. Luego, se dibuja una línea horizontal y se cuenta el número de puntos de intersección con la gráfica de la función. Si el resultado es igual a 1, se retorna true, lo que indica que la función tiene una inversa. En caso contrario, se retorna false.

Cuál es el proceso para sacar la inversa de una función

La inversa de una función es una herramienta importante en matemáticas que nos permite encontrar la entrada original a partir de la salida de una función. Esto es especialmente útil cuando queremos resolver ecuaciones o encontrar valores desconocidos.

El proceso para sacar la inversa de una función consta de los siguientes pasos:

Paso 1: Determinar la función inicial

Para empezar, necesitamos tener una función inicial de la cual queremos encontrar la inversa. Esta función puede ser cualquier función matemática, como una función lineal, cuadrática, exponencial, trigonométrica, entre otras.

Por ejemplo, consideremos la siguiente función:

f(x) = 2x + 5

Paso 2: Reemplazar la función por "y"

En el segundo paso, reemplazamos la expresión de la función con "y". Usar "y" en lugar de la variable "f(x)" simplificará el proceso de encontrar la inversa más adelante.

Utilizando el ejemplo anterior, reemplazamos "f(x)" por "y":

y = 2x + 5

Paso 3: Intercambiar las variables x e y

En este paso, intercambiamos las variables x e y en la expresión que obtuvimos en el paso anterior. Esto nos ayudará a despejar y (la función inversa) en términos de x.

En nuestro ejemplo, intercambiamos x e y:

x = 2y + 5

Paso 4: Resolver para y

Ahora, vamos a despejar y en términos de x resolviendo la expresión del paso anterior. Para ello, reorganizamos la ecuación para aislar "y" en un lado de la igualdad.

Continuando con nuestro ejemplo:

x - 5 = 2y
y = (x - 5) / 2

Paso 5: Escribir la función inversa

Finalmente, escribimos la función inversa utilizando y como función de x. La función inversa se representa comúnmente añadiendo un "-1" al final de la función original.

En nuestro ejemplo, la función inversa sería:

f-1(x) = (x - 5) / 2

¡Y eso es todo! Ahora tenemos la función inversa de nuestra función original. Podemos utilizar esta nueva función para encontrar los valores originales a partir de los resultados de la función inicial.

Es importante recordar que no todas las funciones tienen una inversa. Para que una función tenga una inversa, debe pasar la prueba de la función uno a uno, lo que significa que cada valor de entrada tiene que tener un valor de salida único.

Cuáles son las propiedades de las funciones inversas

Las funciones inversas son un concepto fundamental en matemáticas que nos permiten encontrar la función original a partir de su inversa. Para entender mejor las propiedades de las funciones inversas, es necesario comprender qué es una función inversa.

Una función inversa es aquella que, aplicada sobre el resultado de otra función, nos devuelve el valor original. En otras palabras, si tenemos una función f(x) y su inversa g(x), entonces se cumple lo siguiente:

f(g(x)) = x
g(f(x)) = x

Por ejemplo, si tenemos una función f(x) = 2x + 3, su inversa g(x) sería aquella función que deshace la operación realizada por f(x). En este caso, la inversa sería g(x) = (x - 3)/2, ya que al aplicar g(f(x)) obtenemos el valor original de x.

Veamos algunas propiedades importantes de las funciones inversas:

Propiedad 1: Las funciones inversas se representan intercambiando x e y

• Si tenemos una función f(x) y su inversa g(x), entonces los puntos (x, y) en la gráfica de f(x) se transforman en (y, x) en la gráfica de g(x).
• Esto significa que si dibujamos la gráfica de f(x) y luego la gráfica de su inversa g(x), obtendremos una línea diagonal simétrica respecto a la recta y = x.

Propiedad 2: La composición de una función con su inversa es igual a la identidad

1. Si tenemos una función f(x) y su inversa g(x), entonces al componerlas (f(g(x))) obtenemos la función identidad, es decir, la función que no hace ningún cambio en los valores de entrada.
2. Esto se puede ver como un proceso en el que aplicamos primero la función g(x) para obtener el valor original de x, y luego aplicamos la función f(x) para recuperar el resultado inicial.

Las funciones inversas nos permiten deshacer una operación matemática realizada por una función. Son representadas intercambiando x e y en la gráfica y su composición resulta en la función identidad. Comprender estas propiedades es fundamental para poder calcular la inversa de una función y mejorar nuestras habilidades matemáticas.

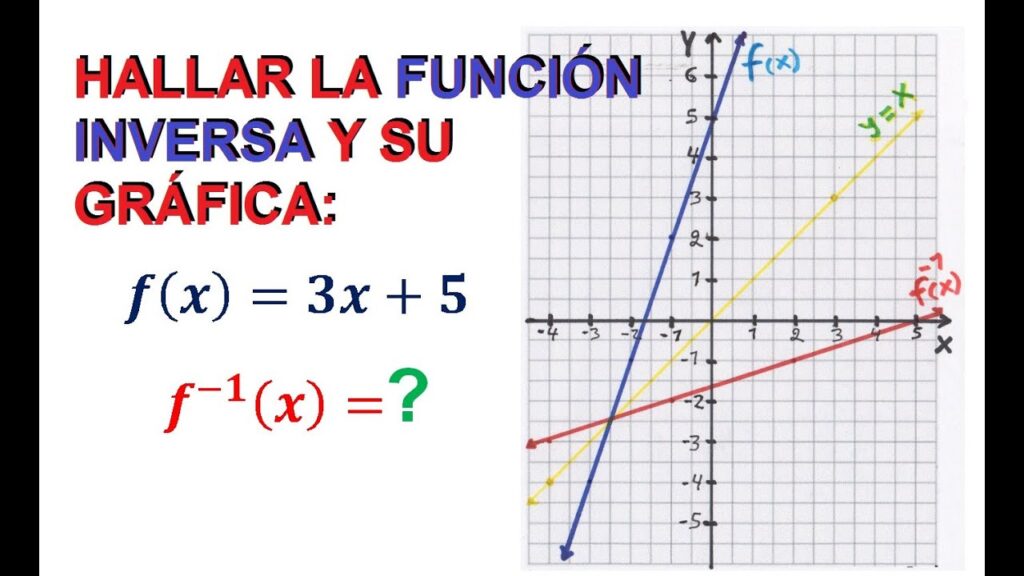
Cómo se representan gráficamente las funciones inversas

Para entender cómo sacar la inversa de una función, es importante tener claro cómo se representan gráficamente las funciones inversas. Las funciones inversas son el resultado de intercambiar el eje x y el eje y en un gráfico de una función dada.

Al graficar una función y su inversa en el mismo plano cartesiano, notarás que las dos gráficas son simétricas con respecto a la línea y = x. Esto significa que si tomas un punto (x, y) en la gráfica de la función original, su punto correspondiente en la gráfica de la inversa será (y, x).

Ejemplo:

Vamos a considerar la función f(x) = 2x + 1. Para graficar esta función, tomamos varios puntos en el plano, sustituimos los valores de x en la función y obtenemos los correspondientes valores de y.


x = -2, f(-2) = -3
x = -1, f(-1) = -1
x = 0, f(0) = 1
x = 1, f(1) = 3
x = 2, f(2) = 5


Ahora, al graficar estos puntos, obtendremos una línea recta en forma de V que pasa por ellos. Esta es la gráfica de la función original f(x) = 2x + 1.

Para obtener la gráfica de la función inversa, simplemente intercambiamos los valores de x y y en los puntos obtenidos anteriormente. Así, obtenemos los siguientes puntos:


x = -3, f_inverse(-3) = -2
x = -1, f_inverse(-1) = -1
x = 1, f_inverse(1) = 0
x = 3, f_inverse(3) = 1
x = 5, f_inverse(5) = 2


Graficando estos puntos, obtenemos otra línea recta en forma de V, pero esta vez invertida. Esta es la gráfica de la función inversa.

Es importante destacar que nem siempre todas las funciones tienen una inversa. Una función debe ser biyectiva para tener una inversa definida. Esto significa que cada valor de x tiene un único valor correspondiente de y, y cada valor de y tiene un único valor correspondiente de x. Si una función no cumple con estas condiciones, no tiene una inversa definida.

Qué aplicaciones tienen las funciones inversas en la vida cotidiana

Las funciones inversas tienen aplicaciones muy relevantes en nuestra vida cotidiana. Aunque en muchas ocasiones no nos demos cuenta, utilizamos las funciones inversas de forma intuitiva para resolver problemas y tomar decisiones.

Una de las aplicaciones más comunes es en la resolución de ecuaciones. Imagina que necesitas calcular el valor de x en una ecuación como 2x + 4 = 10. Para despejar x, debes utilizar la función inversa de la adición y la multiplicación. Restas 4 a ambos lados de la ecuación y luego divides por 2 para encontrar el valor de x. Este proceso se basa en el uso de las funciones inversas de forma implícita.

Otra aplicación práctica de las funciones inversas está en la programación y la ciencia de datos. En estos campos, es necesario analizar grandes cantidades de información y encontrar patrones o tendencias. Las funciones inversas son útiles para revertir procesos matemáticos complejos y así poder entender los datos de una manera más clara.

Además, las funciones inversas también se utilizan en áreas como la física, la ingeniería y las finanzas. Estas disciplinas requieren de cálculos precisos y a menudo deben resolver problemas utilizando funciones inversas específicas, como la función exponencial o la función logarítmica.

Las funciones inversas son parte fundamental de nuestra vida cotidiana y su comprensión puede ayudarnos a resolver problemas de manera más eficiente en diferentes áreas. Ya sea para resolver ecuaciones, analizar datos o realizar cálculos en áreas especializadas, conocer el concepto de función inversa es una herramienta valiosa en nuestras habilidades matemáticas.

Qué técnicas se pueden utilizar para simplificar y resolver problemas relacionados con las funciones inversas

Resolver problemas relacionados con las funciones inversas puede ser un desafío, pero existen varias técnicas que pueden simplificar este proceso. Aquí te presentamos algunas de las más comunes:

1. Encontrar la función inversa

El primer paso para resolver un problema relacionado con las funciones inversas es encontrar la función inversa de la función original. Esto se puede hacer intercambiando las variables en la ecuación y resolviendo para la variable original.

f(x) = y
x = f-1(y)

2. Seguir el procedimiento inverso

Una vez que tienes la función inversa, puedes utilizar el mismo procedimiento que utilizaste para resolver la función original, pero en sentido inverso. Por ejemplo, si utilizaste la regla de los exponentes para resolver una función exponencial, ahora puedes aplicar la regla inversa para resolver la función inversa.

3. Identificar puntos críticos

En algunos casos, puede resultar útil identificar los puntos críticos de la función original y usar esta información para resolver la función inversa. Los puntos críticos son aquellos en los que la función cambia su concavidad o presenta máximo o mínimo local. Al analizar estos puntos, puedes obtener pistas sobre cómo resolver la función inversa.

4. Utilizar gráficas

Las gráficas pueden ser de gran ayuda para visualizar las funciones originales y sus inversas. Si graficas ambas funciones en un sistema de coordenadas cartesianas, puedes identificar patrones y relaciones entre ellas que te pueden ayudar a resolver problemas relacionados con las funciones inversas.

5. Utilizar propiedades y reglas matemáticas

Otra técnica común para resolver problemas de funciones inversas es utilizar propiedades y reglas matemáticas específicas. Esto puede incluir reglas de operaciones algebraicas, propiedades de funciones trigonométricas u otras propiedades matemáticas que sean relevantes para el problema en cuestión.

Aunque estas técnicas pueden ayudarte a simplificar y resolver problemas relacionados con las funciones inversas, es importante recordar que cada situación puede requerir un enfoque único. La práctica constante y la familiarización con diferentes tipos de funciones y sus propiedades te ayudarán a mejorar tus habilidades para resolver este tipo de problemas matemáticos.

Cuáles son los errores comunes al sacar la inversa de una función y cómo evitarlos

La inversa de una función es una operación fundamental en matemáticas que nos permite deshacer los efectos de una función y recuperar el valor original. Sin embargo, calcular la inversa de una función puede ser complicado y propenso a cometer errores si no se tiene cuidado.

Error 1: No verificar si la función es invertible

Antes de intentar sacar la inversa de una función, es importante asegurarse de que la función sea invertible. Una función es invertible si y solo si es biyectiva, es decir, si cada elemento del dominio tiene un único elemento correspondiente en el rango y viceversa. Si intentamos sacar la inversa de una función no invertible, obtendremos un resultado incorrecto o no obtendremos ningún resultado.

Error 2: No encontrar una expresión algebraica explícita

Para calcular la inversa de una función, necesitamos encontrar una expresión algebraica explícita de la función original. Muchas veces, las funciones dadas están definidas por fórmulas complicadas o mediante tablas de valores. Es importante simplificar dichas fórmulas o establecer relaciones entre los valores para obtener una expresión explícita que nos permita calcular la inversa de manera más sencilla.

Error 3: No intercambiar variables y resolver para la variable independiente

Una vez que tenemos una expresión algebraica explícita de la función original, debemos intercambiar las variables y resolver para la variable independiente. La idea es despejar la variable independiente y expresarla en términos de la variable dependiente. Este paso es crucial para obtener la ecuación de la inversa de manera correcta.

Error 4: No verificar si la función obtenida es realmente la inversa

Una vez que hemos obtenido la ecuación de la inversa, es importante verificar si en realidad es la inversa de la función original. Podemos hacerlo comprobando si aplicar la función inversa a los valores obtenidos de la función original nos devuelve los valores originales. Si no es así, es posible que hayamos cometido un error en los pasos anteriores y necesitemos revisar nuestra solución.

Al sacar la inversa de una función es fundamental evitar estos errores comunes para obtener resultados precisos y válidos. Verificar si la función es invertible, encontrar una expresión algebraica explícita, intercambiar variables y resolver para la variable independiente, y verificar si la función obtenida es la inversa son pasos claves para tener éxito en este proceso matemático.

Cuáles son las principales diferencias entre una función y su inversa

Antes de adentrarnos en cómo sacar la inversa de una función, es importante entender las diferencias fundamentales entre una función y su inversa. Esto nos ayudará a comprender mejor el concepto y su aplicación práctica.

1. Dominio y rango

En una función, el dominio representa el conjunto de todos los posibles valores de entrada o argumentos, mientras que el rango representa el conjunto de todos los posibles valores de salida o imágenes. Por otro lado, en la inversa de una función, el dominio se convierte en el rango y viceversa.

Esto significa que si una función mapea un número x a un número y, su inversa mapeará ese mismo número y a x.

2. Composición

Una función puede ser compuesta con otra función para formar una nueva función. Sin embargo, cuando se trata de la inversa de una función, la composición de la función original con su inversa resultará en la función identidad. En otras palabras, la función identidad deja los valores de entrada sin cambios.

3. Gráficamente

Si representamos gráficamente una función en un plano cartesiano, podemos observar la relación entre los valores de entrada y los valores de salida. En una función, cada valor de entrada está asociado a un solo valor de salida. Sin embargo, en la inversa de una función, cada valor de salida está asociado a un solo valor de entrada.

Esto implica que al graficar una función y su inversa, ambas gráficas serán simétricas respecto a la recta y = x. Es decir, si una función tiene un punto (x, y), su inversa tendrá el punto (y, x).

4. Notación

En cuanto a la notación, una función suele representarse como f(x), donde f es el nombre de la función y x es el valor de entrada o argumento. La inversa de una función se denota como f^-1(x), donde f^-1 significa "inversa de f" y x sigue representando el valor de entrada.

Es importante tener en cuenta que f^-1(x) no indica la potencia negativa de f(x), sino que hace referencia a la función inversa.

Ahora que ya conocemos las principales diferencias entre una función y su inversa, podemos adentrarnos en cómo sacar la inversa de una función y expandir nuestras habilidades matemáticas.

Cómo se relacionan las funciones inversas con otros conceptos matemáticos como composición de funciones y dominio y rango

Las funciones inversas son una herramienta poderosa en matemáticas que nos permiten analizar y comprender mejor las relaciones entre distintos conceptos. Una de las formas en las que podemos relacionarlas con otros temas importantes es a través de la composición de funciones.

La composición de funciones es un proceso en el cual se toma una función y se hace actuar sobre los resultados de otra función. Si tenemos dos funciones, f(x) y g(x), la composición de estas se denota como (f ∘ g)(x) o simplemente f(g(x)). En otras palabras, la función resultante de la composición es el resultado de aplicar primero g(x) y luego f(x).

La relación entre la función inversa y la composición de funciones es especial. Si tenemos una función f y su función inversa f⁻¹, entonces al componer ambas obtendremos la función identidad. Es decir, la función que no cambia ningún valor, la función que devuelve el mismo valor que recibe.

Por ejemplo, si tenemos una función f(x) = 2x y su función inversa f⁻¹(x) = x/2, al componer ambas funciones obtendremos (f ∘ f⁻¹)(x) = f(f⁻¹(x)) = f(x/2) = 2(x/2) = x. Así confirmamos que la composición de una función y su función inversa nos da la función identidad.

Otro aspecto interesante relacionado con las funciones inversas es cómo afectan al dominio y rango de una función. El dominio de una función es el conjunto de todos los posibles valores de entrada (x) para los cuales la función está definida. El rango, por otro lado, es el conjunto de todos los posibles valores de salida (y) que la función puede generar.

En el caso de una función inversa, el dominio y el rango de la función original se intercambian. Esto significa que si una función tiene un valor x en su dominio, entonces el correspondiente y estará en el rango de la función inversa. De manera similar, si un valor y está en el rango de la función original, entonces el correspondiente x estará en el dominio de la función inversa.

Este intercambio entre dominio y rango es intuitivo si pensamos en lo que representa una función inversa. Imaginemos que tenemos una función f que toma un número y lo duplica. La función inversa sería una función que toma un número y lo divide por 2 para devolvernos el número original. En este caso, los números que están en el dominio de f estarán en el rango de f⁻¹ y viceversa.

Las funciones inversas son poderosos conceptos matemáticos que nos permiten entender mejor las relaciones entre distintos temas como la composición de funciones y el dominio y el rango. Comprender cómo se relacionan estos conceptos nos ayudará a desarrollar nuestras habilidades matemáticas y resolver problemas más complejos.

La función inversa de una función toma el resultado de la función original y devuelve el valor de entrada original.

Para encontrar la inversa de una función, intercambia las variables x e y en la ecuación de la función original y resuelve para y.

No, una función solo tiene una inversa si es biyectiva, lo que significa que cada valor de entrada corresponde a un único valor de salida.

La función inversa "deshace" lo que hace la función original, devolviendo el número original desde el valor transformado.

No es posible encontrar una función inversa si la función original asigna el mismo valor a varios valores de entrada diferentes (es decir, no es inyectiva).