Descubre la medida precisa del ángulo externo de un icosaedro regular: ¡un dato esencial para tus cálculos geométricos!

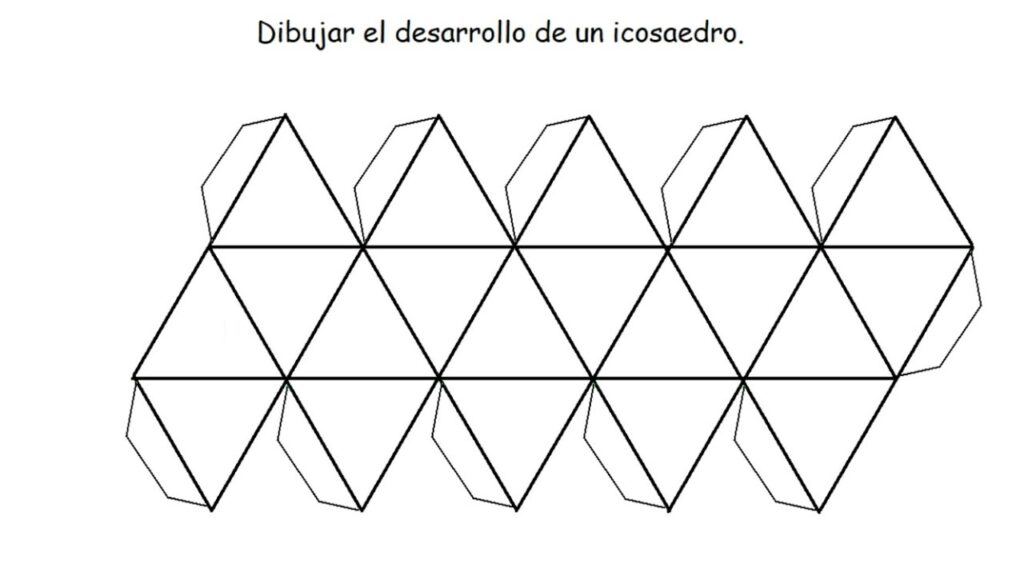
Un icosaedro regular es un poliedro compuesto por 20 caras, todas ellas son triángulos equiláteros. Se trata de uno de los cinco sólidos de Platón y tiene propiedades geométricas muy interesantes. En este artículo nos enfocaremos en la medida precisa del ángulo externo de un icosaedro regular.

En el siguiente texto encontrarás una explicación detallada sobre cómo calcular la medida del ángulo externo de un icosaedro regular. Veremos paso a paso cómo realizar este cálculo y qué fórmula podemos utilizar. Además, te daremos algunos ejemplos numéricos para que puedas aplicar los conocimientos en problemas prácticos. ¡No te pierdas este artículo si quieres aprender más sobre la geometría de los sólidos de Platón!

Qué es un icosaedro regular y cómo se caracteriza

Un icosaedro regular es un poliedro compuesto por 20 caras congruentes, todas ellas formadas por triángulos equiláteros. Este sólido platónico es uno de los cinco poliedros regulares y se caracteriza por tener 12 vértices y 30 aristas.

Cálculo del ángulo externo de un icosaedro regular

El ángulo externo de un poliedro regular es aquel que se forma entre una cara y su vecina. En el caso específico del icosaedro regular, cada una de sus caras está formada por tres triángulos equiláteros. Por lo tanto, el ángulo externo de un icosaedro regular es igual a la suma de los ángulos internos de dos triángulos equiláteros.

La medida de un ángulo interno de un triángulo equilátero es de 60 grados. Por lo tanto, podemos determinar que:

Ángulo externo del icosaedro regular = 60 + 60 = 120 grados

El ángulo externo de un icosaedro regular es de 120 grados.

Importancia del conocimiento del ángulo externo del icosaedro regular

Conocer la medida del ángulo externo de un icosaedro regular es esencial para varios cálculos geométricos. Por ejemplo, si necesitamos calcular el área total de un icosaedro regular, podemos utilizar la fórmula:

Área total del icosaedro regular = 5 * Área de una cara

Donde el área de una cara se puede obtener mediante el cálculo del área de un triángulo equilátero:

Área de una cara = (lado)^2 * √3 / 4

Incluso para cálculos más complejos, como la resolución de problemas de volumen o cálculos de ángulos internos adicionales, el conocimiento del ángulo externo del icosaedro regular es fundamental.

Cuál es la fórmula para calcular el ángulo externo de un icosaedro regular

El ángulo externo de un icosaedro regular puede calcularse utilizando la fórmula: Ángulo Externo = 360° / Número de caras

Donde el número de caras en un icosaedro regular siempre es 20.

Por lo tanto, podemos substituir este valor en la fórmula anterior para obtener: Ángulo Externo = 360° / 20 = 18°

Entonces, el ángulo externo de un icosaedro regular es de 18 grados.

Esta medida es esencial para realizar cálculos geométricos y encontrar ángulos internos y otros elementos correspondientes a un icosaedro. Esto se debe a que los ángulos internos de cualquier poliedro convexo suman un total de 360 grados, y conocer el ángulo externo permite deducir las medidas de los ángulos internos.

Cuál es el valor exacto del ángulo externo de un icosaedro regular en grados

Para calcular el valor exacto del ángulo externo de un icosaedro regular en grados, necesitamos tener en cuenta algunas propiedades básicas de esta figura geométrica.

¿Qué es un icosaedro regular?

Un icosaedro regular es un poliedro compuesto por 20 caras congruentes, todas ellas de forma triangular. Cada una de estas caras es un triángulo equilátero y todos los lados del icosaedro tienen la misma longitud. Además, cada vértice del icosaedro es el punto de encuentro de exactamente tres caras.

Fórmula para calcular el ángulo externo

La fórmula que nos permite calcular el valor del ángulo externo de un poliedro regular en general es:

Ángulo externo = 360° / número de caras

En el caso específico del icosaedro regular, sabemos que consta de 20 caras. Por lo tanto, podemos sustituir este valor en la fórmula:

Ángulo externo = 360° / 20

Realizando la operación, obtenemos:

Ángulo externo = 18°

Significado del ángulo externo en un icosaedro regular

El ángulo externo de un icosaedro regular representa la medida del ángulo formado entre dos caras adyacentes, tomando como referencia el centro del icosaedro. En otras palabras, si en el icosaedro trazamos una línea desde el centro hacia uno de sus vértices, el ángulo externo es el que se forma entre esta línea y una de las caras que comparten dicho vértice.

Conocer este valor es esencial para realizar cálculos geométricos más complejos, como la determinación de longitudes de aristas o áreas de superficies.

Cómo se demuestra la medida precisa del ángulo externo de un icosaedro regular

o.

En resumen, el ángulo externo de un icosaedro regular se calcula dividiendo 360° entre el número de caras en un vértice. En el caso del icosaedro regular, cada vértice está rodeado por 5 caras, por lo que su ángulo externo es de 72°. Conocer esta medida es fundamental para realizar cálculos y comprender mejor las propiedades de este sólido geométrico. Además, esta información puede ser aplicada en diversos campos como la construcción de modelos 3D, la arquitectura y el diseño industrial.

Por qué es importante conocer la medida exacta del ángulo externo de un icosaedro regular en cálculos geométricos

El icosaedro regular es uno de los sólidos platónicos más fascinantes en la geometría. Con sus 20 caras equiláteras y sus ángulos uniformes, es una figura que ha intrigado a matemáticos y arquitectos a lo largo de la historia.

Pero, ¿por qué es importante conocer la medida exacta del ángulo externo de un icosaedro regular en cálculos geométricos?

La respuesta es simple: el ángulo externo de un icosaedro regular es un dato esencial para realizar diversas operaciones y cálculos relacionados con esta figura. Desde cálculos de áreas y volúmenes hasta construcciones y diseños arquitectónicos, el conocimiento preciso de este ángulo nos permite obtener resultados más precisos y eficientes.

En un icosaedro regular, cada uno de sus ángulos externos mide exactamente 72 grados. Esta medida constante nos brinda una base sólida para resolver problemas geométricos y realizar cálculos precisos.

Por ejemplo, si deseamos calcular el área total de un icosaedro regular, podemos utilizar la fórmula A = 5√3 * a^2, donde "A" representa el área total y "a" es la longitud de las aristas. Sabiendo que el ángulo externo mide 72 grados, podemos obtener la altura de cada una de las 20 caras utilizando trigonometría y así evaluar de manera precisa la fórmula del área.

Además, conocer la medida exacta del ángulo externo nos permite realizar construcciones precisas de icosaedros regulares. En arquitectura y diseño, este conocimiento puede ser invaluable para crear estructuras simétricas y estéticamente agradables.

Conocer la medida precisa del ángulo externo de un icosaedro regular es esencial en cálculos geométricos, permitiéndonos obtener resultados más precisos y eficientes en áreas como el cálculo de áreas y volúmenes, y en la construcción y diseño arquitectónico.

Preguntas frecuentes (FAQ)

1. ¿Qué es un icosaedro regular?

Un icosaedro regular es un poliedro formado por 20 caras equilaterales y 12 vértices, donde cada ángulo de las caras mide 60 grados.

2. ¿Cómo se define el ángulo externo de un icosaedro regular?

El ángulo externo de un icosaedro regular es el complemento del ángulo interno de una de sus caras, y su medida es de 120 grados.

3. ¿Para qué es útil conocer la medida del ángulo externo de un icosaedro regular?

Conocer la medida del ángulo externo de un icosaedro regular es esencial para realizar cálculos geométricos precisos, como determinar la distancia entre dos puntos en el espacio tridimensional usando coordenadas esféricas.

4. ¿Cómo se puede calcular la medida del ángulo externo de un icosaedro regular?

La medida del ángulo externo de un icosaedro regular se puede calcular dividiendo 360 grados entre el número de caras del poliedro, en este caso, 20 caras.

5. ¿Existen fórmulas especiales para trabajar con los ángulos externos de poliedros regulares?

No hay fórmulas específicas para trabajar con los ángulos externos de poliedros regulares en general, ya que cada poliedro tiene características y medidas diferentes.