Measure grandes beneficios: cómo sacar las medidas de tendencia central fácilmente

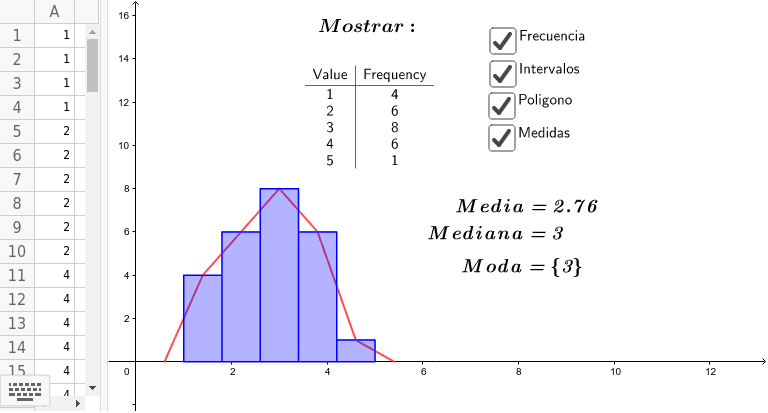
En el análisis de datos, es fundamental poder resumir la información de manera concisa y representativa. Para ello, se utilizan las medidas de tendencia central que permiten conocer cuál es el valor típico o central en un conjunto de datos. Estas medidas nos ayudan a entender mejor los datos y a tomar decisiones más informadas en diversos ámbitos, como la economía, la salud, la educación, entre otros.

Exploraremos las diferentes medidas de tendencia central más comunes, como la media aritmética, la mediana y la moda. Además, aprenderemos cuándo y cómo aplicar cada una de ellas dependiendo del tipo de datos que tengamos y de los objetivos de nuestro análisis. También veremos algunos ejemplos prácticos para comprender mejor su cálculo y utilidad en diferentes situaciones. ¡Acompáñanos en este recorrido por el fascinante mundo de las medidas de tendencia central!

Qué son las medidas de tendencia central

Las medidas de tendencia central son estadísticas descriptivas que nos permiten resumir y representar un conjunto de datos mediante un único valor. Estas medidas nos ayudan a entender el valor típico o central de un conjunto de datos, lo cual puede ser útil para tomar decisiones, comparar grupos o identificar valores atípicos.

Las principales medidas de tendencia central son la media aritmética, la mediana y la moda. Cada una de estas medidas se calcula de manera diferente y nos proporciona información distinta sobre los datos.

La media aritmética

La media aritmética es el promedio de un conjunto de datos. Se calcula sumando todos los valores y dividiendo el resultado entre el número total de elementos. Matemáticamente, se expresa de la siguiente manera:

Media = (x1 + x2 + ... + xn) / n

Donde x1, x2, ..., xn son los valores del conjunto de datos y n es el número de elementos.

La media aritmética es una medida de tendencia central muy utilizada, ya que es sensible a todos los valores del conjunto de datos. Sin embargo, puede ser afectada por valores atípicos, lo cual puede distorsionar su interpretación.

La mediana

La mediana es el valor que se encuentra en la posición central de un conjunto de datos ordenados de menor a mayor. Si el número de datos es impar, la mediana coincide con el valor del centro. Si el número de datos es par, la mediana es el promedio de los dos valores centrales.

Para calcular la mediana, primero se ordenan los datos de menor a mayor. Luego, si el número de datos es impar, se selecciona el valor que se encuentra en la posición (n + 1) / 2. Si el número de datos es par, se selecciona los valores que se encuentran en las posiciones n/2 y (n/2) + 1, y se calcula su promedio.

La mediana es una medida de tendencia central robusta, ya que no se ve afectada por valores atípicos en el conjunto de datos. La mediana proporciona una buena indicación del valor central cuando hay valores extremos o asimetrías en la distribución.

La moda

La moda es el valor que se repite con mayor frecuencia en un conjunto de datos. Puede haber más de una moda si varios valores tienen la misma frecuencia máxima.

La moda es una medida de tendencia central útil cuando queremos conocer cuál es el valor más común en un conjunto de datos. Sin embargo, no siempre es posible calcular la moda, especialmente si los datos son continuos o no tienen repetición.

Las medidas de tendencia central nos permiten resumir y representar la información contenida en un conjunto de datos. La media aritmética, la mediana y la moda son las principales medidas de tendencia central, y cada una de ellas proporciona información diferente sobre los datos. Es importante utilizar estas medidas de manera adecuada, considerando las características de los datos y los objetivos del análisis.

Cuál es la importancia de las medidas de tendencia central en los análisis estadísticos

Las medidas de tendencia central son herramientas clave en los análisis estadísticos, ya que nos permiten resumir y describir la distribución de datos. Estas medidas nos ayudan a comprender dónde se concentran los valores y cuál es el valor típico de un conjunto de datos.

Una medida de tendencia central es un valor que representa un conjunto de datos de manera resumida. Las tres medidas de tendencia central más comunes son la media, la mediana y la moda.

La media

La media es la suma de todos los valores dividida por el número total de valores. Esta medida es particularmente útil cuando queremos conocer el valor promedio de un conjunto de datos. Por ejemplo, si tenemos las edades de cinco personas: 20, 25, 30, 35 y 40, la media sería igual a 30.

La mediana

La mediana es el valor que se encuentra en el centro de un conjunto de datos ordenados. Para obtener la mediana, primero debemos ordenar los valores de menor a mayor y luego seleccionar el valor del medio. En caso de tener un número par de datos, se calcula como la media de los dos valores del centro. Si tenemos los siguientes números: 1, 2, 3, 4, 5, la mediana sería igual a 3.

La moda

La moda es el valor que se repite con mayor frecuencia en un conjunto de datos. Puede haber conjuntos de datos sin moda (cuando no hay valores que se repitan) o conjuntos de datos con múltiples modas (cuando hay varios valores que se repiten con la misma frecuencia máxima). Por ejemplo, si tenemos el siguiente conjunto de números: 2, 4, 4, 6, 7, la moda sería igual a 4.

Estas tres medidas nos dan una idea clara y concisa sobre dónde se encuentran los valores más representativos en un conjunto de datos. Sin embargo, es importante tener en cuenta que ninguna medida de tendencia central puede resumir completamente una distribución de datos. Es por eso que también es útil considerar otras medidas estadísticas, como la desviación estándar o el rango intercuartílico, para obtener una imagen más completa de la variabilidad de los datos.

Qué tipos de medidas de tendencia central existen y cuándo se utilizan cada una

Existen tres tipos principales de medidas de tendencia central: la media aritmética, la mediana y la moda. Cada una se utiliza en diferentes situaciones dependiendo de las características de los datos.

Media aritmética

La media aritmética es el promedio de un conjunto de valores. Se calcula sumando todos los valores y dividiendo el resultado entre el número total de valores. La media aritmética es útil cuando los datos están distribuidos de manera simétrica y no hay valores atípicos que afecten significativamente los resultados. Es una medida comúnmente utilizada en estadística y proporciona un valor representativo del conjunto de datos.

Mediana

La mediana es el valor que divide a un conjunto de datos ordenados en dos partes iguales. Es decir, el 50% de los datos se encuentran por encima de la mediana y el 50% se encuentran por debajo de ella. La mediana es una medida robusta, lo que significa que no se ve afectada por valores atípicos o extremos en los datos. Es especialmente útil cuando los datos están sesgados o tienen valores atípicos, ya que proporciona un valor representativo de la "zona central" del conjunto de datos.

Moda

La moda es el valor que aparece con mayor frecuencia en un conjunto de datos. Puede haber una moda (unimodal) si solo hay un valor que se repite más veces que cualquier otro, o varias modas (multimodal) si hay dos o más valores con igual frecuencia máxima. La moda es útil para identificar los valores más comunes en un conjunto de datos y es especialmente útil cuando se trata de datos cualitativos o categóricos.

Elegir la medida de tendencia central adecuada depende del tipo de datos con los que estemos trabajando y de las características particulares de los mismos. La media aritmética es útil cuando los datos están simétricamente distribuidos y no hay valores atípicos. La mediana es una buena opción cuando los datos están sesgados o tienen valores extremos, ya que es robusta a esas situaciones. Y la moda es especialmente útil para datos cualitativos o categóricos, identificando los valores más comunes.

Cómo calcular la media aritmética y qué información nos proporciona

La media aritmética es una medida de tendencia central que se utiliza para calcular el valor promedio de un conjunto de datos. Se obtiene sumando todos los valores y dividiendo el total entre la cantidad de elementos.

Para calcular la media aritmética, se deben seguir los siguientes pasos:

1. Sumar todos los elementos del conjunto de datos.

suma = elemento1 + elemento2 + ... + elementoN

2. Dividir la suma obtenida entre la cantidad de elementos.

media_aritmetica = suma / cantidad_de_elementos

Por ejemplo, si tenemos el siguiente conjunto de datos: ., podemos calcular la media aritmética de la siguiente manera:

• Sumamos todos los elementos: 5 + 8 + 6 + 10 + 12 = 41
• Dividimos la suma entre la cantidad de elementos: 41 / 5 = 8.2

Entonces, la media aritmética de ese conjunto de datos es igual a 8.2. Esta medida nos proporciona información sobre el valor promedio de los datos. Es una forma de representar el centro del conjunto.

¿Qué información nos proporciona la media aritmética?

La media aritmética nos ayuda a entender el comportamiento general de un conjunto de datos. Nos permite tener una idea de cuál es el valor más representativo o típico.

Además, la media aritmética tiene propiedades matemáticas que nos permiten realizar comparaciones entre diferentes conjuntos de datos. Por ejemplo, podemos calcular la media de dos conjuntos y determinar cuál tiene un valor promedio mayor.

Sin embargo, es importante tener en cuenta que la media aritmética puede ser influenciada por valores extremos o atípicos en el conjunto de datos. Es una medida sensible a los valores más altos o más bajos, lo que puede afectar su interpretación en ciertos casos.

Cómo calcular la mediana y qué nos indica sobre los datos

La mediana es una medida de tendencia central que se utiliza para identificar el valor medio de un conjunto de datos ordenados. A diferencia de la media aritmética, que se calcula sumando todos los valores y dividiendo por el número total de observaciones, la mediana se encuentra en el punto medio del conjunto de datos.

Para calcular la mediana, primero debemos organizar los datos en orden ascendente o descendente. Si tenemos un número impar de observaciones, la mediana será el valor que ocupe la posición central. Por ejemplo, si tenemos 9 observaciones, la mediana corresponderá al quinto valor cuando los datos estén ordenados.

En caso de tener un número par de observaciones, la mediana se calcula como el promedio de los dos valores centrales. Por ejemplo, si tenemos 10 observaciones, la mediana será igual a la suma del quinto y sexto valor dividido entre dos.

Por qué utilizar la mediana

La mediana es una medida útil cuando tenemos datos sesgados o con valores atípicos (outliers). A diferencia de la media aritmética, la mediana no se ve influenciada por estos valores extremos, por lo que brinda una mejor representación del centro de los datos.

Además, la mediana también es utilizada cuando los datos no tienen una distribución simétrica. Mientras que la media aritmética es más sensible a las colas de la distribución, la mediana permite estimar el valor central de manera más robusta ante este tipo de situaciones.

Otra ventaja de utilizar la mediana es que nos ofrece información relevante sobre la dispersión de los datos. Si en un conjunto de datos la mediana y la media aritmética diffieren significativamente, esto indica que los datos están muy dispersos.

Cómo calcular la mediana en Excel

En Microsoft Excel, podemos calcular la mediana utilizando la función MEDIANA. Esta función toma como argumento un rango de celdas que contiene nuestros datos y devuelve el valor de la mediana.

=MEDIANA(rango_de_celdas)

Por ejemplo, si tenemos los siguientes datos en las celdas A1:A10:

10, 15, 20, 25, 30, 35, 40, 45, 50, 55

Podemos calcular la mediana con la siguiente fórmula:

=MEDIANA(A1:A10)

El resultado sería 30, que corresponde al valor central del conjunto de datos ordenado.

Qué es la moda y cómo se calcula? ¿Es siempre relevante en el análisis de datos

La moda es una medida de tendencia central que representa el valor o valores más frecuentes en un conjunto de datos. Se calcula determinando la frecuencia de cada valor y seleccionando aquel o aquellos con mayor frecuencia.

En el análisis de datos, la moda puede ser relevante en ciertos casos para comprender la distribución de los datos y detectar patrones. Sin embargo, su utilidad puede depender del tipo de datos y el objetivo del análisis.

Cálculo de la moda

Para calcular la moda, se deben seguir los siguientes pasos:

1. Ordenar los datos de menor a mayor.
2. Determinar la frecuencia de cada valor.
3. Seleccionar aquel o aquellos con mayor frecuencia.

Si hay un único valor con la frecuencia más alta, se dice que el conjunto de datos tiene una moda. Si hay múltiples valores con la misma frecuencia más alta, se dice que el conjunto de datos tiene varias modas.

Es importante mencionar que la moda solo puede calcularse en variables que presenten valores discretos o categóricos. En variables continuas, como las medidas de tiempo o peso, no existe un valor específico que pueda tener mayor frecuencia.

Relevancia en el análisis de datos

La moda puede ser relevante en diversos contextos:

• Identificación de valores atípicos: Al analizar la moda, es posible identificar si existen valores que ocurren con mayor frecuencia y pueden considerarse como valores atípicos.
• Análisis de distribuciones: La moda puede ayudar a comprender la forma de la distribución de los datos. Por ejemplo, una distribución con varias modas puede indicar la presencia de subgrupos o patrones específicos.
• Segmentación de audiencias: En el ámbito del marketing y la investigación de mercado, conocer la moda de ciertos atributos demográficos puede ser útil para segmentar a la audiencia y dirigir estrategias específicas a cada grupo.

Sin embargo, es importante tener en cuenta que la moda puede no ser suficiente para obtener una imagen completa de la distribución de los datos. Es recomendable complementar su análisis con otras medidas de tendencia central, como la media y la mediana, así como con gráficos descriptivos.

Cuáles son las ventajas y desventajas de utilizar cada medida de tendencia central

Las medidas de tendencia central son herramientas estadísticas que nos permiten resumir y entender un conjunto de datos. Cada medida tiene sus ventajas y desventajas, lo que significa que es importante elegir la medida adecuada para cada situación.

Media aritmética

La media aritmética es la medida de tendencia central más comúnmente utilizada. Se calcula sumando todos los valores de un conjunto de datos y dividiendo el resultado por el número total de valores. La ventaja de utilizar la media aritmética es que utiliza todos los datos disponibles en el cálculo, lo que la hace representativa del conjunto completo. Sin embargo, esta medida puede verse afectada por valores atípicos o extremos, lo que puede distorsionar el resultado.

Mediana

La mediana es la medida de tendencia central que divide al conjunto de datos en dos partes iguales, es decir, el 50% de los datos están por encima y el 50% están por debajo. Esta medida es útil cuando el conjunto de datos contiene valores atípicos o extremos, ya que no se ve tan afectada por ellos como la media aritmética. Sin embargo, la mediana no utiliza todos los datos disponibles en el cálculo, lo que puede hacerla menos precisa en algunas situaciones.

Moda

La moda es el valor o valores que aparecen con mayor frecuencia en un conjunto de datos. Esta medida es útil cuando se quiere identificar los valores más comunes, y puede ser especialmente útil en conjuntos de datos con una distribución bimodal o multimodal. Sin embargo, la moda no siempre está definida o puede no ser representativa del conjunto completo de datos.

Media geométrica

La media geométrica se utiliza cuando los datos están en una escala logarítmica o cuando nos interesa calcular tasas de crecimiento compuesto. Se calcula como el producto de todos los valores elevados a la potencia de uno dividido por el número total de valores. Esta medida es robusta frente a valores atípicos y extremos, pero solo es adecuada para ciertos tipos de datos.

Cómo interpretar las medidas de tendencia central en diferentes escenarios y contextos

Las medidas de tendencia central son estadísticas descriptivas que nos permiten resumir un conjunto de datos en un solo valor representativo. Estas medidas, como la media, la mediana y la moda, son muy útiles en diferentes escenarios y contextos para entender mejor la distribución de los datos y realizar comparaciones entre distintas muestras o poblaciones.

La media

La media es quizás la medida de tendencia central más utilizada. Se calcula sumando todos los valores de los datos y dividiendo el resultado por el número total de observaciones. Es importante tener en cuenta que la media es sensible a valores atípicos, ya que su cálculo se basa en todos los valores de los datos. Por lo tanto, si tenemos valores extremadamente grandes o pequeños en nuestra muestra, la media puede verse afectada significativamente.

La mediana

A diferencia de la media, la mediana no se ve afectada por valores atípicos. La mediana es el valor central de una serie de datos ordenados de menor a mayor. En otras palabras, es el valor que divide al conjunto de datos en dos partes iguales, con tantos valores mayores como menores. Esta medida es especialmente útil cuando nuestros datos contienen valores extremos que podrían sesgar la interpretación de la media.

La moda

La moda representa el valor o valores que se repiten con mayor frecuencia en un conjunto de datos. A diferencia de la media y la mediana, la moda no tiene en cuenta el valor absoluto de los datos, sino su frecuencia. Si existen varios valores que se repiten con la misma frecuencia máxima, se dice que hay una distribución bimodal o multimodal. Esta medida es especialmente útil cuando queremos identificar los valores más comunes en nuestra muestra.

Comparando las medidas de tendencia central

Cuando queremos comparar dos o más conjuntos de datos, las medidas de tendencia central pueden ser muy útiles para tener una idea rápida de las diferencias entre ellos. Por ejemplo, si queremos comparar la altura promedio de hombres y mujeres, podemos calcular la media y la mediana de ambas muestras y analizar las diferencias. Del mismo modo, si queremos conocer cuál es la moda de las marcas de automóviles más vendidas, podemos realizar un análisis estadístico basado en la frecuencia de ventas.

Las medidas de tendencia central nos ofrecen información valiosa sobre nuestros datos y nos ayudan a interpretarlos de manera más fácil y precisa. Dependiendo del escenario y el contexto, podemos utilizar la media, la mediana o la moda para resumir nuestros datos y realizar comparaciones significativas. No olvidemos que estas medidas son solo una parte del análisis estadístico y siempre debemos complementarlas con otras herramientas y métodos para obtener una visión más completa y precisa de nuestros datos.

Qué herramientas o software se pueden utilizar para calcular rápidamente las medidas de tendencia central

Hay una variedad de herramientas o software disponibles en el mercado que pueden ayudarte a calcular rápidamente las medidas de tendencia central. A continuación, se presentan algunas de las opciones más populares:

Microsoft Excel

Microsoft Excel es una herramienta muy utilizada y ampliamente disponible que ofrece diversas funciones estadísticas para calcular medidas de tendencia central. Puedes utilizar las funciones PROMEDIO, MEDIANA y MODA para obtener los valores correspondientes. También puedes utilizar el comando ANÁLISIS DE DATOS para calcular medidas como la media geométrica, armónica y cuadrática.

R

R es un lenguaje de programación y entorno de software especialmente diseñado para análisis estadístico y gráfico. Es una opción excelente para realizar cálculos complejos de medidas de tendencia central, ya que ofrece una amplia gama de paquetes y bibliotecas estadísticas. Con R, puedes aplicar funciones como mean(), median() y mode() para obtener las medidas deseadas.

Python con las bibliotecas NumPy y pandas

Python es un lenguaje de programación muy popular y versátil, y cuando se combina con las bibliotecas NumPy y pandas, se convierte en un poderoso conjunto de herramientas para el análisis de datos. Con NumPy, puedes utilizar las funciones mean(), median() y mode() para calcular medidas de tendencia central. Pandas, por otro lado, ofrece una funcionalidad adicional para trabajar con conjuntos de datos estructurados, lo que facilita aún más el cálculo y análisis de medidas de tendencia central.

SPSS

SPSS es un software estadístico ampliamente utilizado en investigaciones y análisis de datos. Ofrece una interfaz gráfica fácil de usar que te permite calcular rápidamente medidas de tendencia central utilizando métodos tradicionales. Con SPSS, puedes realizar análisis descriptivos e inferenciales, así como generar tablas y gráficos para visualizar los resultados.

Statistical Analysis System (SAS)

SAS es otro software estadístico popular utilizado en diversos campos, como la salud, la ciencia social y la industria. Puedes utilizar SAS para calcular medidas de tendencia central utilizando sus procedimientos estadísticos. SAS también ofrece una gran cantidad de opciones y funciones personalizables para realizar análisis estadísticos más avanzados.

Existen varias herramientas y software disponibles para calcular rápidamente las medidas de tendencia central. La elección de la herramienta adecuada dependerá de tus necesidades específicas, preferencias personales y nivel de experiencia en programación y análisis estadístico.

Cómo sacar conclusiones y tomar decisiones basadas en las medidas de tendencia central obtenidas

Las medidas de tendencia central son herramientas estadísticas fundamentales para analizar conjuntos de datos y obtener conclusiones relevantes. Estas medidas nos permiten tener una idea clara de cómo se distribuyen los valores en un conjunto de datos y nos ayudan a tomar decisiones informadas basadas en la información obtenida.

Media aritmética

Una de las medidas de tendencia central más utilizadas es la media aritmética, que se calcula sumando todos los valores y dividiendo el resultado entre el número total de elementos en el conjunto de datos. Esta medida nos proporciona un punto de referencia promedio del conjunto de datos, lo que nos permite tener una idea general de su nivel central.

Por ejemplo, supongamos que tenemos un conjunto de datos con las calificaciones de un examen en una escala del 1 al 10. Si calculamos la media aritmética de estas calificaciones, obtendremos un valor numérico que representa el promedio de todas las calificaciones. Este valor nos puede indicar si los estudiantes obtuvieron resultados cercanos a la media, por encima de la media o por debajo de ella.

Mediana

Otra medida de tendencia central muy utilizada es la mediana, que consiste en encontrar el valor medio en un conjunto de datos ordenados. En otras palabras, la mediana divide el conjunto de datos en dos partes iguales y nos brinda una perspectiva de los valores centrales.

Continuando con el ejemplo anterior, si tenemos las calificaciones de un examen ordenadas de menor a mayor, la mediana será el valor que se encuentra exactamente en el medio. Esto nos proporcionaría información sobre cuántos estudiantes obtuvieron calificaciones por encima o por debajo de la mediana, lo cual es útil para comprender la distribución de las calificaciones en el conjunto de datos.

Moda

La moda es otra medida de tendencia central que se refiere al valor o valores más frecuentes en un conjunto de datos. En otras palabras, la moda nos indica cuál es o cuáles son los "números de moda". Esto puede ser especialmente útil cuando queremos identificar patrones claros o elementos destacados en un conjunto de datos.

Por ejemplo, si tenemos un conjunto de datos con las edades de un grupo de personas y encontramos que la edad más común es 30 años, esto nos indicaría que este rango de edad tiene una mayor representación dentro del grupo. La moda nos ayuda a identificar rápidamente los valores más frecuentes y hacer inferencias sobre ellos.

Las medidas de tendencia central nos permiten tener una visión clara y concisa de la distribución de los datos en un conjunto y nos ayudan a sacar conclusiones relevantes y tomar decisiones informadas basadas en esta información. Las medidas de tendencia central más utilizadas son la media aritmética, la mediana y la moda, cada una proporcionando diferentes perspectivas sobre el conjunto de datos. Al utilizar estas medidas de manera adecuada, podemos maximizar nuestros beneficios al analizar conjuntos de datos y realizar conclusiones precisas.

Preguntas frecuentes (FAQ)

1. ¿Qué es la media aritmética?

La media aritmética es el promedio de un conjunto de números.

2. ¿Cómo se calcula la mediana?

La mediana es el valor medio en un conjunto de datos ordenados de menor a mayor.

3. ¿Qué es la moda?

La moda es el valor que aparece con mayor frecuencia en un conjunto de datos.

4. ¿Cuál es la diferencia entre la varianza y la desviación estándar?

La varianza mide la dispersión de los datos con respecto a la media, mientras que la desviación estándar es la raíz cuadrada de la varianza.

5. ¿Cómo interpretar el coeficiente de correlación?

El coeficiente de correlación mide la relación lineal entre dos variables. Un valor cercano a 1 indica una correlación positiva fuerte, mientras que un valor cercano a -1 indica una correlación negativa fuerte.