Descubre cuanto miden los ángulos internos de un triángulo y mejora tus conocimientos matemáticos

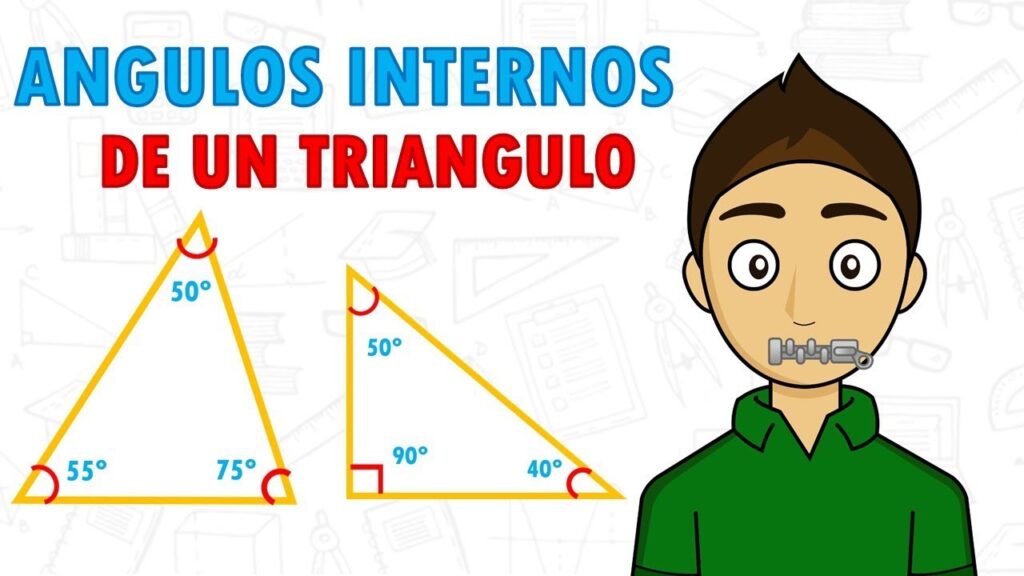
Los triángulos son una de las figuras geométricas más básicas y fundamentales en las matemáticas. Están compuestos por tres lados y tres vértices, y su estudio ha sido objeto de atención desde la antigüedad. Una de las características más importantes de los triángulos son sus ángulos internos, que determinan la forma y características de la figura.

Te contaremos cuánto miden los ángulos internos de un triángulo y cómo se pueden calcular. Exploraremos las propiedades matemáticas y fórmulas que nos permiten determinar los ángulos de esta figura. Además, te mostraremos ejemplos prácticos y te daremos algunos consejos útiles para comprender y aplicar estos conceptos en tus futuros estudios matemáticos.

Cuál es la definición de ángulo interno en un triángulo

En geometría, un triángulo es una figura plana compuesta por tres segmentos de recta que se intersectan en tres puntos distintos llamados vértices. Cada uno de estos vértices forma dos ángulos internos con los otros dos vértices.

Los ángulos internos de un triángulo son aquellos formados por dos segmentos del triángulo que comparten un punto final en uno de los vértices. Estos ángulos están ubicados dentro del triángulo y su suma siempre será igual a 180 grados.

Para visualizarlo mejor, se puede trazar una línea que contenga un ángulo interno de un triángulo y extenderla hasta que corte al lado opuesto del triángulo. La línea resultante será una transversal que divide al triángulo en dos ángulos externos y uno interno.

Fórmula para calcular la suma de los ángulos internos de un triángulo

La fórmula general para calcular la suma de los ángulos internos de un triángulo es:

Suma de ángulos internos = 180 grados

Esta fórmula se aplica a todos los triángulos, independientemente de que sean equiláteros, isósceles o escalenos.

Propiedades de los ángulos internos de un triángulo

• La suma de los ángulos internos de cualquier triángulo siempre será igual a 180 grados.
• En un triángulo equilátero, los tres ángulos internos son iguales y miden 60 grados cada uno.
• En un triángulo isósceles, dos de los ángulos internos son iguales y el tercer ángulo es diferente. La suma de los ángulos iguales siempre será mayor a 90 grados.
• En un triángulo escaleno, los tres ángulos internos son diferentes y no hay una relación específica entre ellos.

Conocer la medida de los ángulos internos de un triángulo es fundamental en geometría y trigonometría, ya que se utilizan en una amplia gama de problemas y ecuaciones.

Cómo se calcula la suma de los ángulos internos de un triángulo

Para calcular la suma de los ángulos internos de un triángulo, podemos utilizar la siguiente fórmula:

Suma = 180 grados

Esta fórmula nos ayudará a determinar la suma total de los ángulos internos de cualquier tipo de triángulo, ya sea equilátero, isósceles o escaleno.

Un triángulo equilátero tiene tres lados iguales y sus ángulos internos también son iguales. Por lo tanto, cada uno de los ángulos internos de un triángulo equilátero mide exactamente 60 grados.

En el caso de un triángulo isósceles, que tiene dos lados iguales y dos ángulos iguales, podemos utilizar la fórmula anterior para calcular la medida del tercer ángulo interno. Por ejemplo, si dos de los ángulos miden 40 grados cada uno, podemos restar su suma total (80 grados) de 180 grados para obtener la medida del tercer ángulo interno: 100 grados.

Por último, en un triángulo escaleno, los tres lados y los tres ángulos internos pueden tener medidas diferentes. En este caso, podemos utilizar la fórmula de la suma de los ángulos internos para determinar su valor total.

Es importante tener en cuenta que esta fórmula solo es válida para triángulos planos. En geometría euclidiana, la suma de los ángulos internos de un triángulo siempre será igual a 180 grados, sin importar su forma o tamaño.

Cuánto mide cada uno de los ángulos internos en un triángulo equilátero

En un triángulo equilátero, los tres ángulos internos tienen la misma medida. Esto se debe a que cada uno de los lados del triángulo equilátero es congruente entre sí, lo que implica que los ángulos opuestos a esos lados también son congruentes.

Para calcular la medida de cada uno de los ángulos internos en un triángulo equilátero, podemos utilizar la siguiente fórmula:

Medida de cada ángulo interno = 180° / Cantidad de ángulos

En un triángulo equilátero, tenemos tres ángulos internos, por lo tanto:

Medida de cada ángulo interno = 180° / 3

Resolviendo esta ecuación, obtenemos:

Medida de cada ángulo interno = 60°

Por lo tanto, en un triángulo equilátero, cada uno de los ángulos internos mide 60 grados.

Cuánto miden los ángulos internos en un triángulo isósceles

En un triángulo isósceles, aquel que tiene al menos dos lados congruentes, los ángulos internos también tienen propiedades especiales.

Recordemos que la suma de los ángulos internos de cualquier triángulo es siempre igual a 180 grados. En el caso de un triángulo isósceles, podemos determinar la medida de sus ángulos internos utilizando la siguiente fórmula:

Ángulo = (180 - Base) / 2

Donde "Base" representa el ángulo correspondiente a la base del triángulo. Dado que los otros dos ángulos también son congruentes en un triángulo isósceles, podemos denominarlos como "Ángulo A" y "Ángulo B". La base, por otro lado, se puede identificar como "Ángulo C".

Si conocemos la medida de uno de los ángulos de la base, podemos calcular la medida de los otros dos ángulos utilizando la fórmula anteriormente mencionada. Por ejemplo, si sabemos que el Ángulo C mide 60 grados, podemos calcular los otros dos ángulos de la siguiente manera:

Ángulo A = (180 - 60) / 2 = 60 grados
Ángulo B = (180 - 60) / 2 = 60 grados

Así, en este caso particular, todos los ángulos internos del triángulo isósceles miden 60 grados.

Cuánto miden los ángulos internos en un triángulo escaleno

En un triángulo escaleno, los ángulos internos tienen medidas diferentes. No hay dos ángulos iguales en este tipo de triángulo. Para calcular la medida de cada ángulo interno, podemos utilizar la fórmula matemática (180 / número de lados) * (número de lados - 2).

Veamos un ejemplo: supongamos que tenemos un triángulo escaleno con tres lados. Aplicando la fórmula anterior, obtenemos (180 / 3) * (3 - 2) = 60. Por lo tanto, cada uno de los ángulos internos tiene una medida de 60 grados.

Es importante destacar que en un triángulo escaleno, los ángulos pueden tener diferentes medidas, pero siempre sumarán 180 grados. Esto se debe a la propiedad de la suma de los ángulos internos de un triángulo, que establece que la suma de los tres ángulos es siempre igual a 180 grados.

Además, cabe mencionar que aunque los ángulos internos de un triángulo escaleno no tengan una medida específica como en el triángulo equilátero, siguen manteniendo relaciones proporcionales entre sí. Por ejemplo, si un ángulo es más grande que otro, los lados opuestos a estos ángulos también serán proporcionales.

Cuáles son las propiedades de los ángulos externos de un triángulo

Los ángulos externos de un triángulo tienen propiedades interesantes que vale la pena explorar. Para entender estas propiedades, primero necesitamos saber qué son los ángulos externos.

¿Qué son los ángulos externos de un triángulo?

En un triángulo, los ángulos externos son aquellos que se encuentran fuera del triángulo pero que comparten un vértice con uno de sus ángulos internos. Es decir, son los ángulos formados por una de las prolongaciones de los lados del triángulo y el lado adyacente a ese vértice.

Para visualizar esto mejor, imaginemos un triángulo ABC. Si prolongamos uno de sus lados, digamos AC, hasta que se cruza con la prolongación del lado AB, obtendremos un ángulo externo en el vértice A. De manera similar, podemos obtener los otros dos ángulos externos en los vértices B y C del triángulo.

Se denota como A', B' y C' a los vértices correspondientes a los ángulos externos de los vértices A, B y C respectivamente.

Propiedades de los ángulos externos de un triángulo

Ahora que sabemos qué son los ángulos externos, podemos explorar algunas de sus propiedades:

• La suma de los ángulos externos de un triángulo es siempre 360 grados. Esto significa que si sumamos los tres ángulos externos de cualquier triángulo, obtendremos un total de 360 grados.
• Los ángulos externos son suplementarios a los ángulos internos opuestos. Es decir, si consideramos un ángulo interno de un triángulo y su correspondiente ángulo externo, la suma de estos dos ángulos siempre será igual a 180 grados. Por ejemplo, en el triángulo ABC, el ángulo interno en A y el ángulo externo en A' serán suplementarios.
• Si tomamos los ángulos externos de un triángulo y los restamos alrededor de un punto completo (360 grados), obtendremos un ángulo completo en ese punto. Esto significa que si sumamos los ángulos externos de un triángulo formado por los vértices A', B' y C', obtendremos un ángulo completo en el punto donde se intersectan las prolongaciones de los lados del triángulo original.

Aplicaciones de los ángulos externos de un triángulo

El estudio de los ángulos externos de un triángulo tiene diversas aplicaciones dentro de las matemáticas y otras áreas:

• En trigonometría, los ángulos externos pueden utilizarse para resolver problemas relacionados con la ubicación o dirección de objetos en un plano.
• En geometría plana, los ángulos externos pueden utilizarse para demostrar teoremas y propiedades sobre los triángulos.
• En física, los ángulos externos pueden utilizarse para analizar el movimiento de un objeto en un plano y determinar su trayectoria.

Los ángulos externos de un triángulo tienen propiedades importantes que nos permiten comprender mejor las relaciones entre los diferentes elementos de un triángulo. Su estudio es fundamental en matemáticas y tiene aplicaciones prácticas en diversas áreas del conocimiento.

Preguntas frecuentes (FAQ)

1. ¿Cuánto suman los ángulos internos de un triángulo?

Los ángulos internos de un triángulo suman siempre 180 grados.

2. ¿Todos los triángulos tienen ángulos internos iguales?

No, los ángulos internos de un triángulo pueden ser diferentes dependiendo de sus medidas.

3. ¿Cómo se calcula la medida de un ángulo interno en un triángulo?

La medida de un ángulo interno en un triángulo se puede calcular dividiendo el perímetro del triángulo entre 3.

4. ¿Qué tipo de triángulo tiene ángulos internos de 90 grados?

Un triángulo con ángulos internos de 90 grados se llama triángulo rectángulo.

5. ¿Qué tipo de triángulo tiene todos sus ángulos internos iguales?

Un triángulo con todos sus ángulos internos iguales se llama triángulo equilátero.